N Traveling Salesman Problem
Permasalahan TSP Traveling Salesman Problem adalah permasalahan dimana seorang salesman harus mengunjungi semua kota dimana tiap kota hanya dikunjungi sekali dan dia harus mulai dari dan kembali ke kota asal. Permasalahan ini diilhami oleh.

Two Types Of Open Loop Travelling Salesman Problem A Classic Open Download Scientific Diagram
The traveling salesman problem is a classic problem in combinatorial optimization.
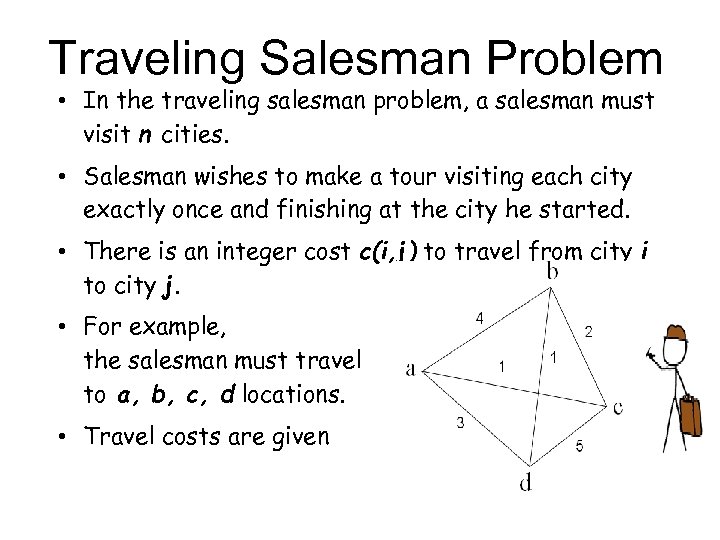
N traveling salesman problem. This route is called a Hamiltonian Cycle and will be explained in Chapter 2 The traveling salesman problem can be divided into two types. TRAVELLING SALESMAN PROBLEM Travelling salesman problem adalah suatu permasalahan dalam bidang diskrit dan optimasi kombinatorial. This problem is to find the shortest path that a salesman should take to traverse through a list of cities and return to the origin city.
The Travelling Salesman Problem TSP is the challenge of finding the shortest yet most efficient route for a person to take given a list of specific destinations. A weighted graph is a graph in which each edge is assigned a weight representing the time distance or cost of traversing that edge. Both of the solutions are infeasible.
The Traveling Salesman Problem De nition. There are approximate algorithms to solve the problem though. Brute force takes more time to compute the cost to solve TSP.
A Hamilton circuit is a circuit that uses every vertex of a graph once. Travelling Salesman Problem TSP. The challenge of the problem is that the traveling salesman wants to minimize the total length of the trip.
Travelling Salesman Problem TSP. The statement is relatively simple. Tujuannya adalah menentukan rute dengan jarak total atau biaya yang paling minimum.
The traveling salesman problem can be described as follows. TSP G f t. The problems where there is a path between.
We can use brute-force approach to evaluate every possible tour and select the best one. Note the difference between Hamiltonian Cycle and TSP. THE TRAVELING SALESMAN PROBLEM 2 1 Statement Of The Problem The traveling salesman problem involves a salesman who must make a tour of a number of cities using the shortest path available and visit each city exactly once and only once and return to the original starting point.
G V E a complete graph f is a function V V Z t Z G is a graph that contains a traveling salesman tour with cost that does not exceed t. Travelling salesman problem is the most notorious computational problem. Note the difference between Hamiltonian Cycle and TSP.
For each number of cities n the number of paths which must be explored is n. A complete graph K N is a graph with N vertices and an edge between every two vertices. It is very hard to find an optimal solution for travelling salesman problem because of that it is also known as NP-complete.
In fact there is no polynomial-time solution available for this problem as the problem is a known NP-Hard problem. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once. We introduced Travelling Salesman Problem and discussed Naive and Dynamic Programming Solutions for the problem in the previous post.
Sebagai permasalahan kombinatorial persoalan ini tergolong memilingi kemungkinan jawaban yang sangat banyak. There are n-12 possible tours in the undirected form of the problem - n-1 instead of n since it doesnt matter which node you start at and you divide by two since eg. For three nodes A B C the tour Ato Bto Cto A is the same as the tour Ato Cto Bto A.
There can be many possible optimal solutions. Which means we have to try all possible permutation combination. Therefore total time complexity is O n2 n O n O n 2 2 n Space complexity is also number of sub-problems which is O n2 n Program for Travelling Salesman Problem in C.
Traveling Salesman Problem. Each sub-problem will take O n time finding path to remaining n-1 nodes. The traveling salesman problem is what is known as a toy problem in the sense that it is not necessarily interesting in and of itself but perfectly encapsulates a question shared by other more sophisticated versions of the problem and that it can be used to give simple demonstrations of methods of solution such as an algorithm based on virtual ants.
Given a set of cities and distance between every pair of cities the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. It is a well-known algorithmic problem in the fields of computer science and operations research. For n number of vertices in a graph there are n - 1.
The Hamiltoninan cycle problem is to find if there exist a tour that. If we solve recursive equation we will get total n-1 2 n-2 sub-problems which is O n2 n. The traveling salesman problem is solved if there exists a shortest route that visits each destination once and permits the salesman to return home.
The list of cities and. Given a set of cities and distances between every pair of cities the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.
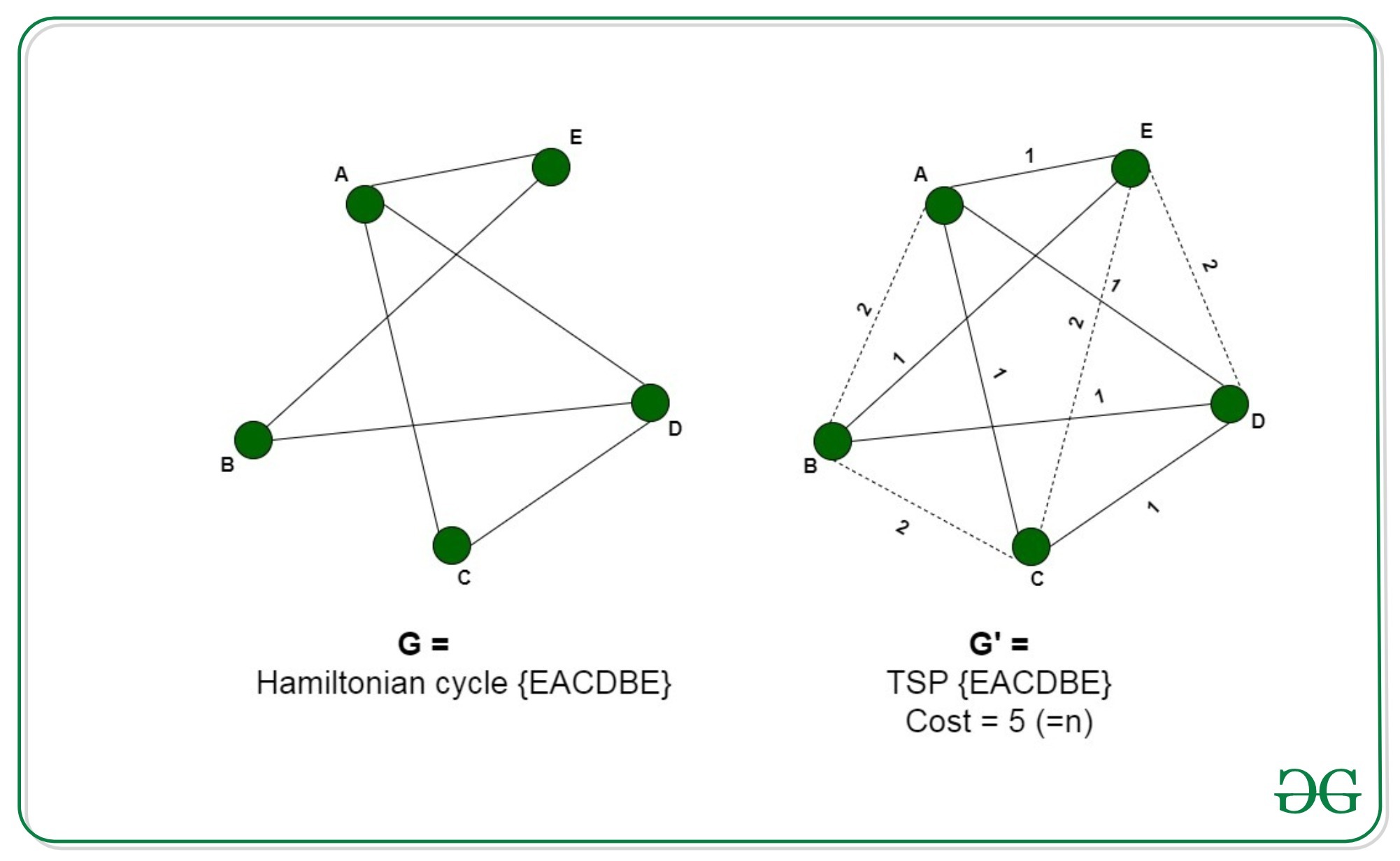
Proof That Traveling Salesman Problem Is Np Hard Geeksforgeeks

Chapter 10 The Traveling Salesman Problem

Traveling Salesman Problem Tsp
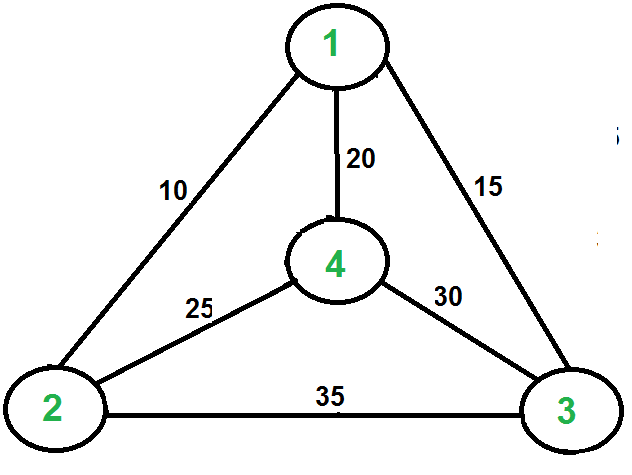
Travelling Salesman Problem Set 1 Naive And Dynamic Programming Geeksforgeeks

Cse 5311 Algorithm Design And Analysis Traveling Salesman

Pdf A Genetic Simplified Swarm Algorithm For Optimizing N Cities Open Loop Travelling Salesman Problem Semantic Scholar

Figure1 The Traveling Salesman Problem Tsp State Space For 4 Cities Download Scientific Diagram
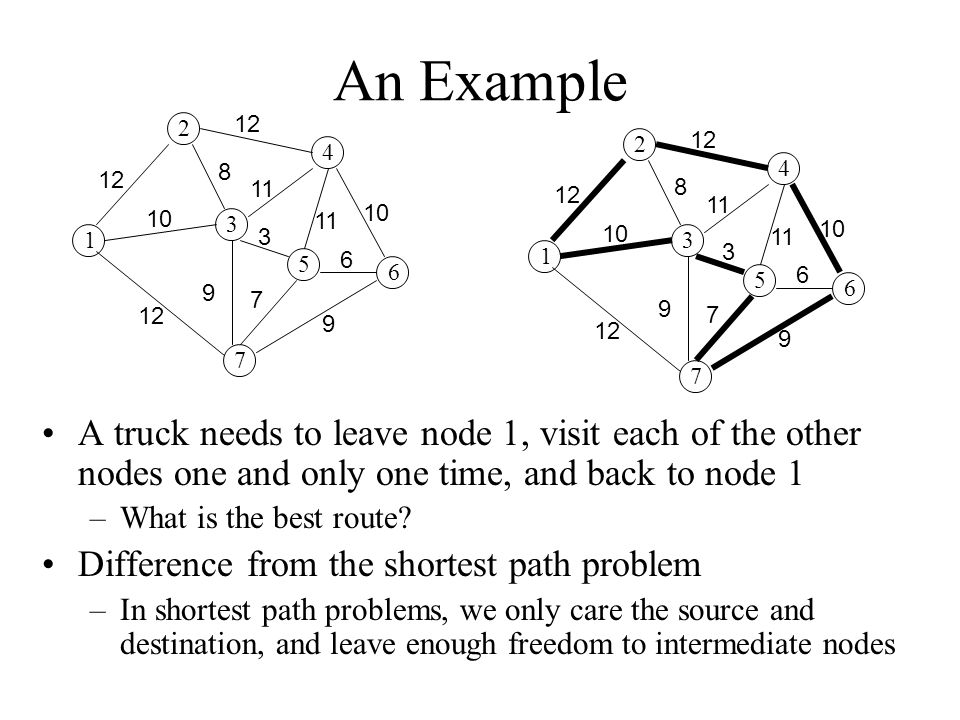
Traveling Salesman Problem Tsp Ppt Video Online Download

Tutorial Introduction To Traveling Sales Man Problem Tsp N Why It Is Np Hard Youtube

Traveling Salesperson Problem Brilliant Math Science Wiki
Posting Komentar untuk "N Traveling Salesman Problem"