N Traveling Salesman

April 17, 2021 Posting Komentar

Each sub-problem will take O n time finding path to remaining n-1 nodes. The Travelling Salesman Problem TSP is the challenge of finding the shortest yet most efficient route for a person to take given a list of specific destinations.

Chapter 10 The Traveling Salesman Problem

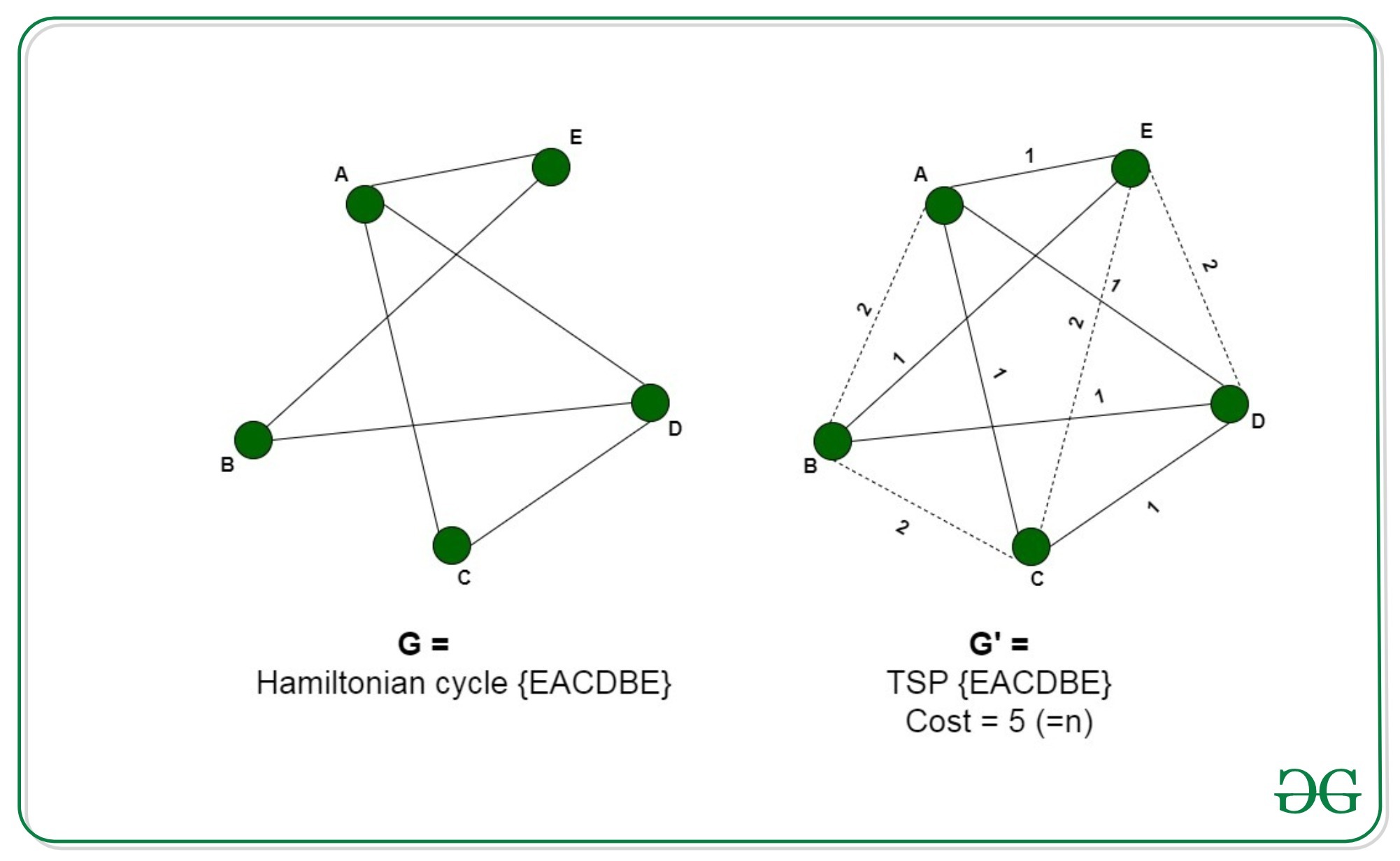
A Hamilton circuit is a circuit that uses every vertex of a graph once.

N traveling salesman. Travelling salesman Problem TSP is one in every off the benchmark and previous issues in applied science and research. Travelling Salesman is a 2012 intellectual thriller film about four mathematicians solving the P versus NP problem one of the most challenging mathematical problems in history. The time complexity with the DP method asymptotically equals N².

It is a well-known algorithmic problem in the fields of computer science and operations research. My attempt was using induction. If we solve recursive equation we will get total n-1 2 n-2 sub-problems which is O n2 n.

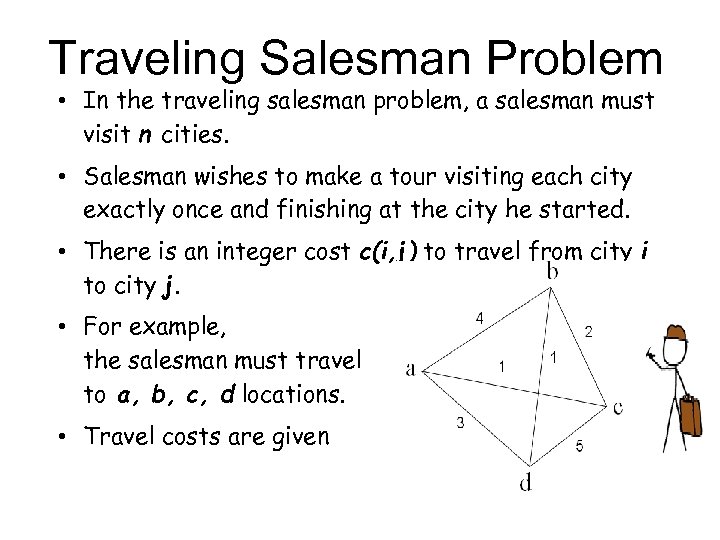
Tujuannya adalah menentukan rute dengan jarak total atau biaya yang paling minimum. 2 distinct tours for a ETSP on n points. He wants to travel to each destination exactly once and return home taking the shortest total route.

Given a set of cities and distances between every pair of cities the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. If n 3 then we have a triangle and there is only one tour. The dynamic programming or DP method guarantees to find the best answer to TSP.

Assume that there are n 1. Therefore total time complexity is O n2 n O n O n 2 2 n Space complexity is also number of sub-problems which is O n2 n Program for Travelling Salesman Problem in C. Agent good.

However its time complexity would exponentially increase with the number of cities. Travelling Salesman Problem TSP. Following are different solutions for the traveling salesman problem.

Penyelesaian Travelling Salesman Problem dengan Algoritma Heuristik Filman Ferdian - 13507091 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha 10 Bandung e-mail. 1 Consider city 1 as the starting and ending point. Commercial traveller or traveller.

So I start by. Which one is it. Permasalahan TSP Traveling Salesman Problem adalah permasalahan dimana seorang salesman harus mengunjungi semua kota dimana tiap kota hanya dikunjungi sekali dan dia harus mulai dari dan kembali ke kota asal.

SO the general answer I come across on the internet is n-12. Let P be the transition matrix between the routes according to the 2-opt procedure. For n number of vertices in a graph there are n - 1.

There can be many possible optimal solutions. But it would seem to be n or at least n-1. Professions a salesman who travels within an assigned territory in order to sell merchandise or to solicit orders for the commercial enterprise he represents by direct personal contact with customers and potential customers.

Each voyage can be represented as a graph G VE where each destination including his home is a. The traveling salesman problem I. N is a graph with N vertices and an edge between every two vertices.

3 Calculate cost of every permutation and keep track of minimum cost permutation. Traveling Salesman solution in c - dynamic programming solution with O n 2n. The question is to show that there are n 1.

A traveling salesman wishes to go to a certain number of destinations in order to sell objects. Traveling Salesman synonyms - 42 Words and Phrases for Traveling Salesman. So n-12 cant hold.

It has been proven that a quick travelling salesman algorithm if one exists could be. Note the difference between Hamiltonian Cycle and TSP. Using namespace stdEstimated Reading Time.

4 Return the permutation with minimum cost. Brute force takes more time to compute the cost to solve TSP. A weighted graph is a graph in which each edge is assigned a weight representing the time distance or cost of traversing that.

We can use brute-force approach to evaluate every possible tour and select the best one. The title refers to the travelling salesman problem an optimization problem that acts like a key to solving other mathematical problems that are thought to be hard. The Hamiltonian cycle problem is to find if there exists a tour that visits every city exactly once.

It is very hard to find an optimal solution for travelling salesman problem because of that it is also known as NP-complete. 2 Generate all n-1. 2 distinct tours for a Euclidean traveling salesman problem ETSP on n points.

The goal is to hunt out the shortest tour that visits every town throughout a given list specifically once then returns to the beginning town 1. Travelling salesman problem is the most notorious computational problem. Which means we have to try all possible permutation combination.

If you have 2 cities you would have 1 path.

Cse 5311 Algorithm Design And Analysis Traveling Salesman